|
|
牛顿法解方程需要先给定一个初值x0,将该值赋值给变量x
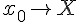
然后反复执行代码:
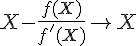
其中f'(x)是f(x)对x的导函数,可以用手求,也可以利用
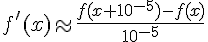
打入计算器,10^-5也可以换成其他比较小的数,只要不超过计算器的精确度就不会影响最终结果。
此程序还可以精简一下:
先将x0赋值给Ans(这个都会吧~)
然后反复执行代码:
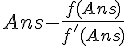
=================================================
牛顿法解方程效率相当高
我们可以假设根为ξ,xi为第i次执行语句后的X的值,理论分析可得
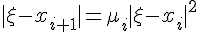
其中,μi由方程和初值决定
例如:要解方程
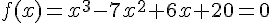
初值x0=-1.5
对于此函数,理论上可以分析出,μi<0.5对于一切正整数i成立(这点是关键,并且几乎所有方程都能得出类似结论),并且
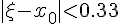
于是有
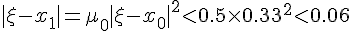
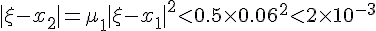
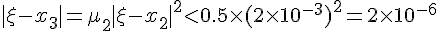
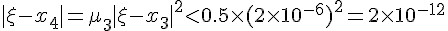
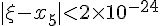
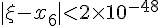
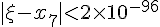
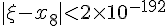
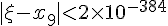
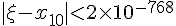
这就是说,对此方程来说,要让精确度达到计算器的精度,只需要重复执行代码4次,如果用电脑进行高精度运算,只需执行代码10次就可以精确到小数点后至少767位(由于理论分析时进行了放大处理,所以实际精确度可达八百多位有效数字),这就是指数爆炸的威力
=================================================
想更多了解牛顿法,可以参见以下书籍(我全没读过)
Hildebrand,Introduction to Numerical Analysis,McGraw-Hill Book Co.,1956
Householder,Principles of Numerical Analysis,McGraw-Hill Book Co.,1953
Whittaker&Robinson,The Calculus of Observations,Blackie and Sons,Ltd.,1929 |
评分
-
查看全部评分
|